應用傳染型餘震序列與地震動模型進行地震活動與場址震度預報:以2022年9月台東地震序列為例
謝銘哲1、詹忠翰1, 2、馬國鳳1, 3、顏銀桐4、陳俊德4、陳達毅5, 6、廖怡雯7, 8
1國立中央大學地震災害鏈風險評估及管理研究中心
2國立中央大學地球科學學系
3中央研究院地球科學研究所
4財團法人中興工程顧問社防災科技研究中心
5中央氣象署地震測報中心
6台北市立大學地球環境暨生物資源學系
7GNS Science, Lower Hutt, New Zealand
8School of Earth and Environment, University of Canterbury, Christchurch, New Zealand
大規模地震後往往伴隨許多餘震,這些餘震可能帶來較大的地震動(ground motion),甚至引發地震次生災害。因此,透過地震預報(earthquake forecasting)並結合精確的地震動或其對應的震度(seismic intensity)估算,評估大地震後數小時至數天內餘震對特定場址(例如核能電廠、高科技與精密製造業產線、政府機關等)可能再次遭遇高震度衝擊的機率,除了保全重要設施之餘,對於保障人命之人員疏散、整體供應鏈支援運作策略與即時分派救災資源等面向皆具有重要助益。此外,這些作為預期能提升地震災害應變整備機制,強化面對震災的韌性。
本研究(Hsieh et al., 2024)參考Zhuang (2011)對於地震活動預報原型架構,採用基於統計學理論之傳染型餘震序列(Epidemic-Type Aftershock Sequence, ETAS, 如Ogata, 1988),該模型基於點過程理論(point process theory)之自激發型霍克斯過程(Hawkes' mutual excitation process),經由蒐集地震目錄並計算大量地震事件在空間中各網格點位置之條件強度函數(conditional intensity function, CIF),透過CIF反應該網格位置的地震活動趨勢,其組成包含背景地震與叢集地震活動兩項,而叢集項結合統計地震學常用之地震規模對次數關係(即Gutenberg-Richter Law)、主震後餘震次數隨時間衰減率(即Omori-Utsu Formula),以及主震觸發餘震之空間機率密度函數共同組成。藉由ETAS模型並搭配即時地震定位資料,我們能夠及時計算反應地震活動變化之CIF,進一步以該函數模擬大地震後的可能餘震分布,圖一即為我們針對2022年9月的台東地震序列進行即時CIF計算,並與接下來一天之內規模3以上的地震事件分佈進行比較,顯示CIF變化與實際觀測地震分佈高度符合,足以作為地震預報的基礎。而後,透過基於ETAS模型進行地震活動模擬,產生大量虛擬地震事件,這些地震事件具有一定規模與時空分布,透過應用地震動模型(Ground Motion Model, GMM),代入虛擬地震的位置與規模,以及合適的場址條件參數(例如VS30),即可計算所關注場址的地震動參數(如Peak Ground Acceleration, PGA或震度);上述模擬地震活動的歷時(例如一天)可視為預報的時間視窗,多次模擬則可視為對虛擬地震活動進行多次採樣,進而形成機率曲線,反應場址在預報區間內可能遭遇到的震度機率,圖二即為我們計算台東地震序列對TTN測站的震度機率預報曲線,和實際觀測到的震度發生次數有相當高的符合程度。
經由上述簡介,不難了解即時地震預報是具有相當程度可行性,對於大地震後的餘震分布與關注場址所造成的衝擊,皆可以統計學模式進行預估,而2022年台東地震序列是一個很好的示例,驗證本研究論述的即時系統具有實務應用價值。然而,大地震後產生餘震即時地震定位資料品質,以及小地震定位數量不足所造成的地震目錄資料缺失(missing data),皆有可能顯著影響ETAS模型參數,增加預報地震活動的不確定性;此外,本研究目前採用的是2維、基於點震源的ETAS模型,對於地震在深度方向的分布,以及具有較大破裂尺度的大地震後餘震分布描述存有較大不確定性,未來仍須仰賴更精緻的ETAS模型以精進地震預報成效。
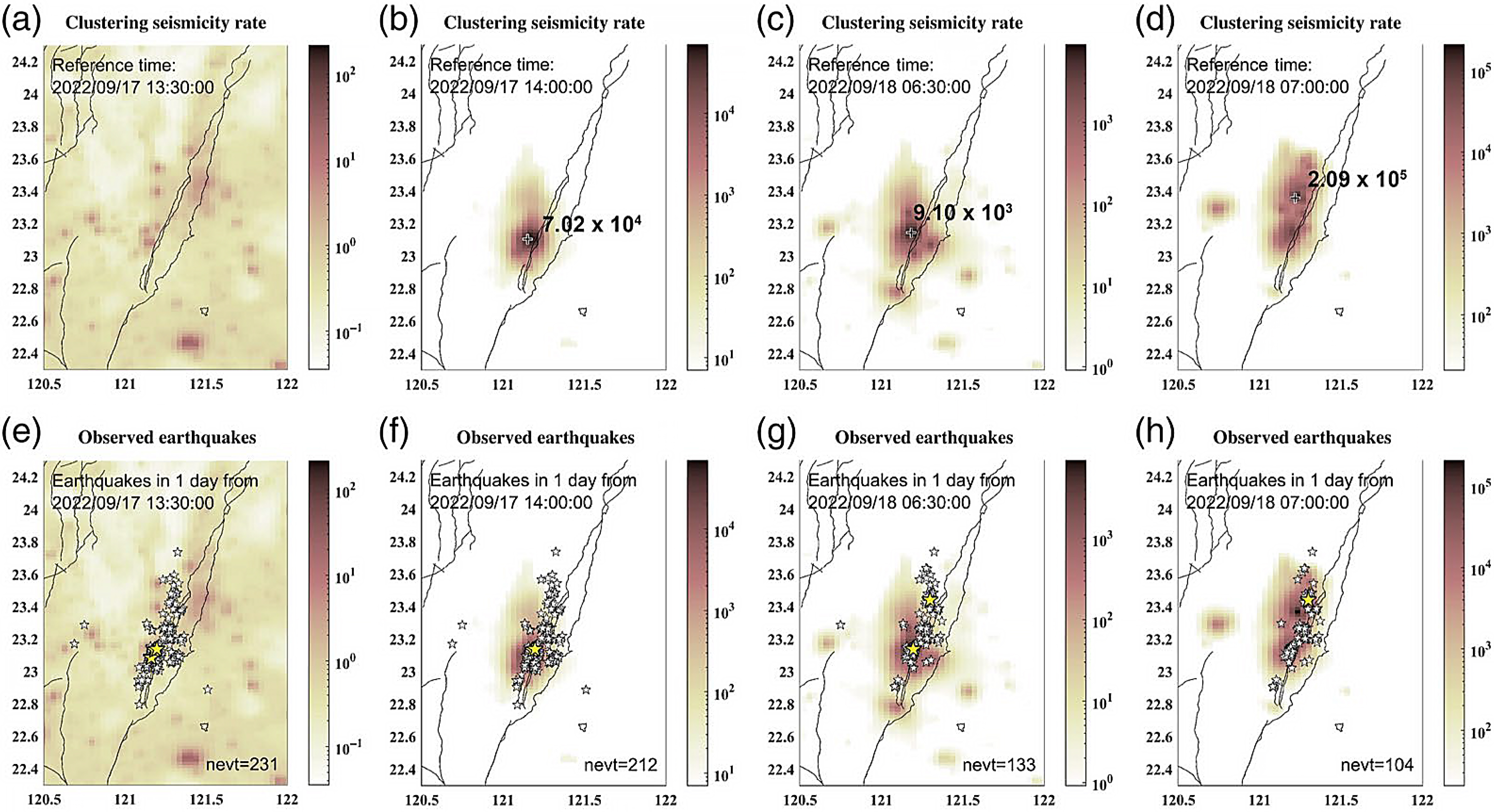
圖一、2022年9月台東地震序列之CIF變化(a) – (d),與CIF計算時刻起一日內地震活動比較(e) – (h),各圖色階表示CIF量值,而星號則表示規模3以上地震,黃色星號則是規模6以上地震。(b) – (d)中,CIF最大值標示於圖面最大值發生處;而(e) – (f)中,觀測地震數量(nevt)標示於左下角。
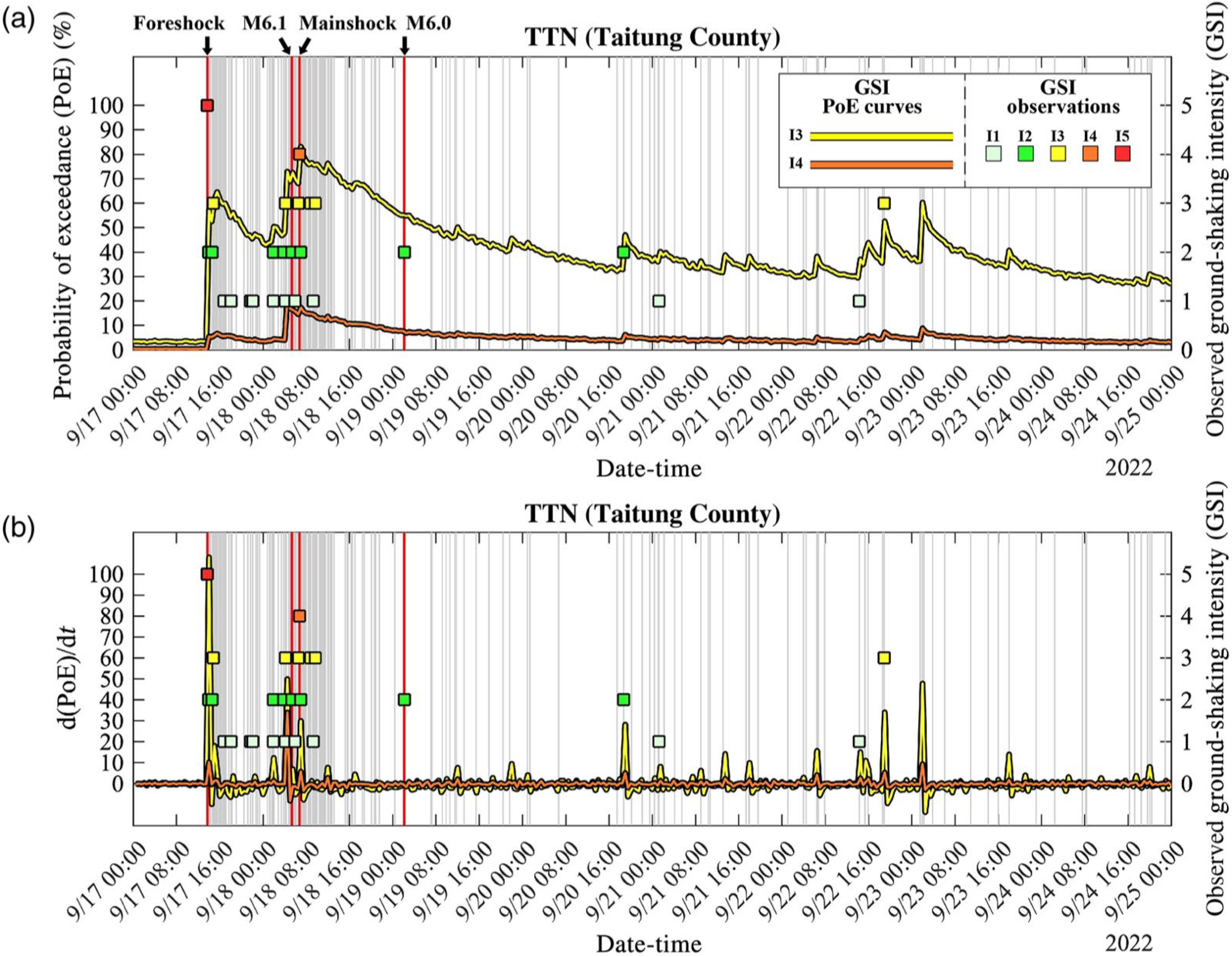
圖二、(a)為TTN測站之震度3與震度4機率預報曲線,以及方形代表在TTN測站的實際觀測震度;(b)為對機率曲線取一次時間導數,圖中各峰值位置可視為發報時刻,提醒有關單位注意餘震將帶來的地震動衝擊。
參考文獻
Hsieh, M.-C., Chan, C.-H., Ma, K.-F., Yen, Y.-T., Chen, C.-T., Chen, D.-Y., & Liao, Y.-W. M. (2024). Toward Real-Time Ground-Shaking-Intensity Forecasting Using ETAS and GMM: Insights from the Analysis of the 2022 Taitung Earthquake Sequence. Seismological Research Letters, 95(6), 3264–3277. https://doi.org/10.1785/0220240180
Ogata, Y. (1988). Statistical Models for Earthquake Occurrences and Residual Analysis for Point Processes. Journal of the American Statistical Association, 83(401), 9–27. https://doi.org/10.1080/01621459.1988.10478560
Zhuang, J. (2011). Next-day earthquake forecasts for the Japan region generated by the ETAS model. Earth, Planets and Space, 63(3), 207–216. https://doi.org/10.5047/eps.2010.12.010